If you spend any time reading the literature on mathematical modeling, you’ll quickly encounter some version of the phrase:
We build mathematical models of the real world in order to explain, predict, or control.
Usually, you’ll find such language as part of a definition of mathematical modeling or of a fairly high-level description of the process. But often, this language isn’t revisited when examples of mathematical modeling are described. This language is often left by the wayside and it’s up to the reader to puzzle out what a given mathematical model was intended to do. Once you have some experience, this isn’t hard, but for the novice, it can be confusing and since the whole point of mathematical modeling is to accomplish one or more of these three goals, it is important for the new modeler to develop some facility with these concepts. So, today, I thought we’d explore the ideas of “explain, predict, or control,” and give concrete examples of each case. Hopefully this will help clarify these purposes of mathematical modeling in your mind and give you a framework for thinking about the purposes of your modeling activities in new cases.
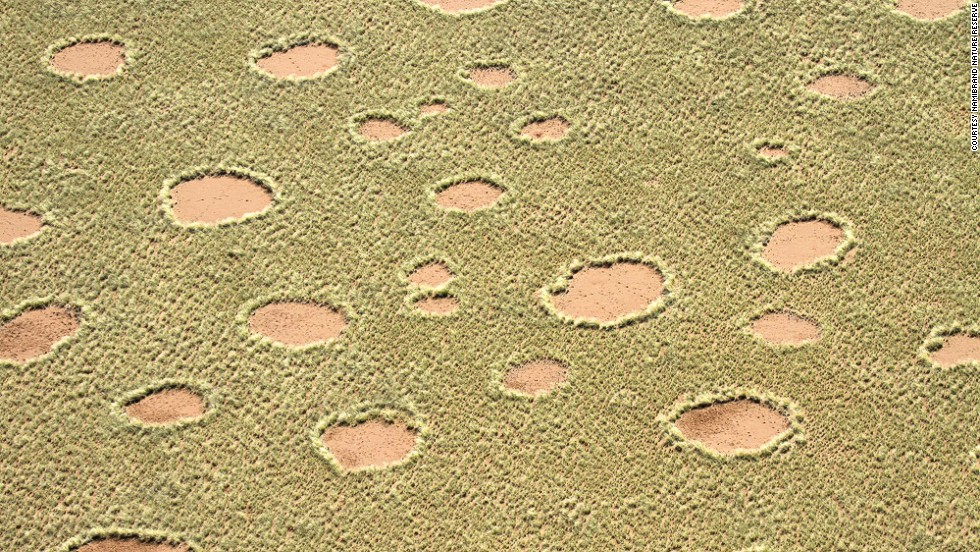
Let’s start with the notion of constructing a mathematical model to explain. This is the case that is most clearly and directly bound together with the scientific process. As our example, let’s return to our investigation of “Fairy Circles” that we discussed here and here. Recall that what we were trying to understand was the origin of so-called “Fairy Circles,” or large, circular, regular clearings in the desert:
The observation was that these were roughly circular and roughly uniform in size. There was no apparent reason for their appearance, hence the invoking of “fairies” as an explanation. Now, this is pretty clearly a situation that calls out for a model that explains. We could ultimately think about a model that predicts their appearance and shape, but it is hard to get excited about a model along those lines that doesn’t also explain. Now, it is important to make sure we understand how mathematical modeling works when we’re seeking to explain. This, again, is where we connect deeply to science. We can imagine that there are lots of different possible mechanisms that would lead to the presence of these circles. That is, we can hypothesize many explanations for the presence of these circles. But, how do we test these hypotheses? An experimental test, in this case, is very difficult to conceive of and likely very expensive and time consuming. That’s a perfect situation in which to bring out the tool of mathematical modeling. Instead of an experiment, what we do is take our hypothesis and build a mathematical model of the purported mechanism for the creation of the circles. We then analyze our model to see if in fact the mathematization of that hypothesis leads to a model that predicts what we observe. If it does, that increases the odds that our hypothesis is correct. Note, it’s not a proof of our hypothesis! It only increases the probability that the hypothesis is correct and gives us more confidence that we have found the likely explanation.
Next, let’s think about what a mathematical model looks like when we want to predict. For this one, let’s return to our discussion of the “tipping bucket/water park” system. Recall that here, we had a bucket held slightly off-center on an axle with water flowing into the bucket.
Periodically, the bucket would become unstable, tip, spill the contained water, and then return to the upright position and repeat. In this case, there is less mystery and less of a calling for an explanation. We can see that the system is mechanically driven, we have intuition about the changing stability, and we can see how it empties and resets. Here, what we want is to be able to predict the period of oscillation, given, for example, the physical properties of the system. That is, if we know the rate at which water flows into the bucket, the mass of the bucket, the volume and shape of the bucket, and the location of the axle, we’d like to be able to predict the interval of time in between tipping of the bucket. We’d like to be able to make this prediction for any given set of parameters for the bucket and perhaps be able to use this to design buckets that tip at different intervals. In this case, to accomplish this, we still make a hypothesis, namely that Newton’s Laws of Mechanics are governing the behavior of the system. But, it’s not really a hypothesis that we’re testing. Here, we have tremendous confidence in the hypothesis a priori. Rather, we’re accepting this hypothesis, mathematizing, and using the results of our analysis to make predictions about the world for systems we haven’t seen yet. Yes, we must still compare the results of our model to those of our observed system to validate. But here, the validation is more along the lines of making sure we did the mechanics and the mathematics correctly and less along the lines of testing the hypothesis that Newton’s Laws apply.
Finally, let’s think about the notion of using a mathematical model to control some real-world system. Let’s note that for both of the systems considered above, we can think about using the models we develop for control in some sense. In the case of Fairy Circles, once we’ve fully explained, we can look for parameters in our model that we can change in the real-world and that would produce different size circles, or perhaps, no circles at all. In the case of the tipping bucket, we can imagine changing the size of the bucket or the rate of the water flow and since we can predict how the period of oscillation will change, this gives us control over the system. These are certainly both examples of how we can use a mathematical model to control. But, I want to give you one other example that perhaps more clearly highlights this idea of using a mathematical model for control. Take a moment and watch this video clip:
This video shows the outcome of a project focused on implementing a classic feedback-control system for an “inverted pendulum.” The basic idea is simple and you can try it right now. Take a pencil and balance it by its point on your hand. You’ll likely almost automatically be able to move your hand to keep the pencil upright. The feedback you receive, visual and tactile, about the pencil’s position lets you rapidly adjust the motion of your hand to keep the pencil upright. Now, if you want to build a machine to do this, here’s where you need a mathematical model for control. Here, as with the tipping buckets, you would build a mathematical model based on the laws of mechanics. This model would tell you how your pendulum should move. But, in this model, you would build in an unspecified applied force to the system. Here, this unspecified part would be the motion of the base of the pendulum. By analyzing your model, you would then determine precisely how the base should move to maintain the upright position of the pendulum. This is then what you’d tell your machine to implement. That is, your mathematical model will tell you that if the pendulum has such and such a position and is moving and such and such a rate, you should move your cart in such a manner. That’s instructions that a machine can follow and you’ve now used a mathematical model to control a system in real time. In addition to the ways in which might use a model to control illustrated by the Fairy Circles and the tipping buckets, it’s useful to have this real-time, programmable sense in mind as well.
Hopefully these examples give you a clearer sense of the differences and similarities between building a mathematical model to explain, predict, or control. I encourage you to think through the goals of your models as you build them and as you first encounter a new modeling situation. In upcoming posts, I’ll work to demonstrate each of these three purposes in even more detail with further examples.
John