This week, I’m taking a break from posting and Michelle is taking the lead with an interesting post about her experience learning about mathematical modeling. As someone who has been embedded in the modeling world for 20+ years, it’s this kind of perspective that I’ve come to value greatly in our work together. Hope you’ll enjoy!
John
In 2009, I attended the 19th ICMI Conference focused on Proof and Proving in Mathematics Education in Taipei, Taiwan. While there I heard a memorable talk given by Anna Marie Conner, a mathematics educator, and Julie M. Kittleson, a science educator, called, Epistemic Understandings in Mathematics and Science: Implications for Learning. In their talk, Conner and Kittleson argued that there are similarities in the processes engaged in to legitimize knowledge claims in mathematics and science, but there are also significant differences that must be recognized and understood because have implications for disciplinary learning. The goal of this work was to promote better understandings among teachers and students of how disciplinary knowledge is established in both mathematics and science. They further argued that examining and understanding these connections will lead to valuable insights for teachers and teacher educators in focusing and sharpening both their own understandings and those of their students. Here are some key points:
- While mathematical inquiry makes use of inductive searches for patterns, knowledge is established deductively in mathematics.
- Mathematical proof is the basis of knowledge in mathematics;
- Establishing truth in science is more nebulous.
- Scientific knowledge is constructed by the interplay between theory and data, but truth is never conclusively established. (p. 1-107)
Conner & Kittleson provided two classroom examples, one from mathematics and one from science:
The interplay of inductive and deductive reasoning is apparent in both mathematics and science classrooms. To illustrate, consider two classrooms, one geometry and one physics. Both classes are taught by teachers who strive to align their teaching with the standards (NCTM, 2000; NRC, 1996). In the geometry class, students explore characteristics of a figure with dynamic geometry software that models Euclidean geometry, and develop a hypothesis about some aspect of relationships within that figure. In the science classroom, students explore the motion of a pendulum and develop a hypothesis about the relationship between the pendulum’s length, the mass of the bob, and the time it takes for the pendulum to complete one swing. To this point, at least from the perspective of the students, they have engaged in similar, perhaps almost identical, activities. However, it is at this point that the different epistemological understandings of the specific disciplines must engage. For in mathematics, the student must attempt to deductively prove the veracity of the hypothesis. No amount of experimentation will allow him or her, from a mathematical perspective, to establish the truth of the hypothesis, and once it is proved, it is established as true with no need to re-prove and no possibility of contradiction. In science, on the other hand, the student must carefully craft an experiment to determine whether his or her hypothesis is correct. This experiment may disprove the hypothesis, but it will not prove that it is correct. It may confirm the hypothesis, but that confirmation is tentative, and is subject to the possibility of disconfirming evidence. (p. 1-108)
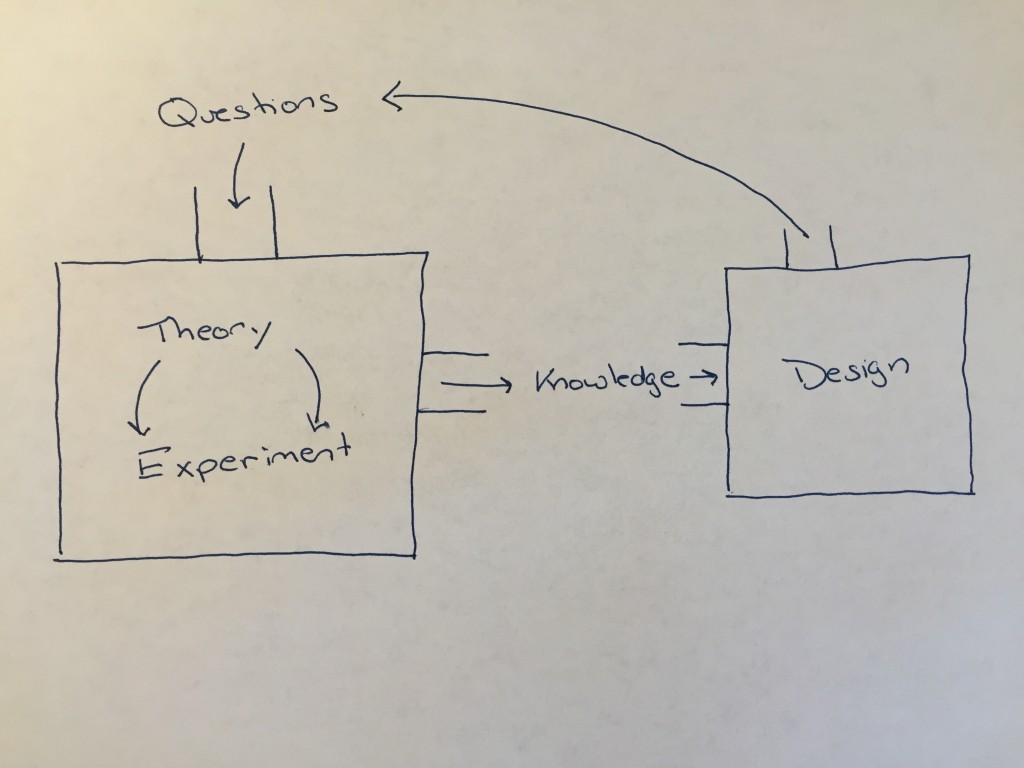
Since I’ve been studying and facilitating professional development on modeling, I’ve had a realization that, while likely obvious to applied mathematicians and scientists, was not as obvious to me, a mathematics educator who is still developing understandings of what it really means to model with mathematics. One of the many realizations that I’ve had is that mathematical modeling, which connects mathematics to the “real world,” behaves more like science than mathematics. How so?
Well, for starters, one engages in mathematical modeling to understand something about reality and/or to help you predict something in the real world. At the same time, the real world is messy, and true modeling tasks are ill-defined.
Because the real world allows for many areas of investigation and requires the modeler to make choices, decisions, and assumptions throughout the process, a mathematical modeling investigation does not culminate in any one “right” model or path to a solution. When people look at the same real-world phenomenon, just as in science, they can have diverse perspectives into the task’s resolution. They will inevitably make different choices and assumptions, and thus, mathematical models are ultimately built based on hypotheses or guesses as to how the real-world system behaves. A mathematical model is therefore judged by the accuracy of its predictions, the power of its explanations, or the simplicity of its implementation. In fact, when evaluating mathematical models, the aphorism of statistician George Box, which essentially says that all models are wrong, but some are useful, can be helpful to keep in mind. That is, we can never “prove” that a mathematical model is “correct.”
As Conner and Kittleson argued, teachers who understand the epistemology of both mathematics and science are in a better position to capitalize on the similarities between math and science and to highlight the subtle and more obvious differences between the two. This has led me to realize that effective teaching of mathematical modeling really does require the development of expertise in both mathematics and science, or at least those aspects of science related to the real-world systems one wants to study in one’s classroom. For this reason, more conversations and collaborations between mathematics and science educators are critical for the development of 21st-century skills.
Michelle