Just spent a great week at NCSM 2016 in Oakland, CA. Wish we could have stuck around for NCTM 2016 across the bay, but sadly, not in the cards this year. Today, I thought I’d share a bit about our session on mathematical modeling for those who couldn’t be there in person.
First, let me share links to a few things. A PDF of our slides from the session can be found here.
We also left the attendees with two handouts that can be found here.
The first handout outlines the key features of mathematical modeling and the key features of the QFT, which I’ll talk about below. The second is a useful worksheet for helping teachers and students engage in meta-thinking about their mathematical modeling work.
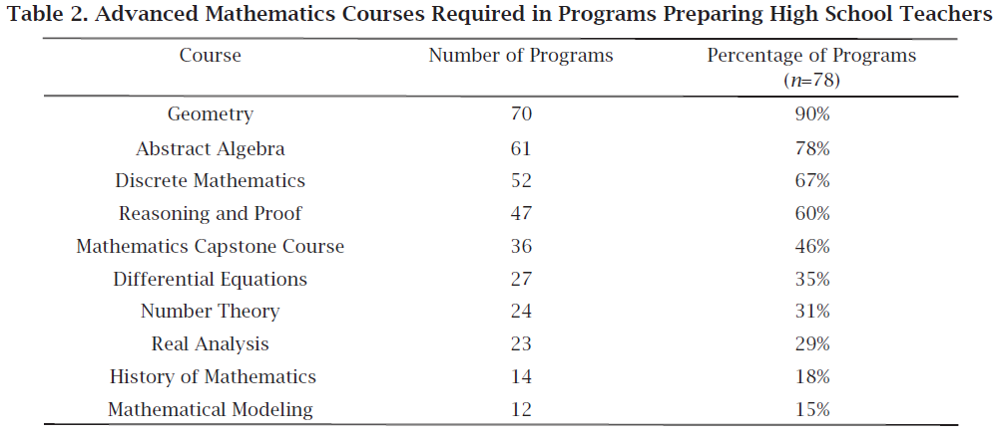
During the opening of our session, Michelle strove to make the following point – it’s not surprising that teachers in the United States are finding the implementation of SMP #4 to be a challenge. She shared the following table which highlights the very small fraction of teacher preparation programs that provide their students with any training in mathematical modeling.
For teachers graduating from one of the 85% of programs that provide no training in mathematical modeling, preparing to teach SMP #4 is like preparing to teach geometry, never having had a course in geometry. In fact, it’s a bit more difficult, since even if someone somehow missed out on a college level course in geometry, they still would have seen it in high school. With modeling, we face the situation where the vast majority of teachers have never seen mathematical modeling at any level in their education. In addition to this issue, Michelle also discussed the huge deficits in secondary mathematics curricula related to mathematical modeling and made the point that a long history of embedding math tasks in pseudo-contexts has left students unprepared to deal with real real-world situations in the math classroom.
In the next part of our session, I spent some time discussing the points we discussed in one of our previous posts. Since at least one of the attendees found a new analogy we used particularly compelling, let me elaborate on that point here (thank @mary_davis_utdc!). When talking about the important fact that mathematical modeling is an iterative process, we discussed the question as to what exactly drives that iteration. For an analogy, I relied on one my favorite things, the lazy river. A special thanks to @mary_davis_utdc for tweeting us this picture after the session!
In a lazy river, you’re just drifting around and around a river in a closed loop, that is in a cycle. But in every such river, at some point along the cycle, you’ll find there are jets that propel the water in a particular direction and keep the cycle moving. In mathematical modeling it’s the “Validate” step that serves as the “jets” of the modeling cycle. Remember, the “Validate” step is where you take the model that you’ve formulated and analyzed and compare its predictions or insight back to the real world. To the extent that your model’s predictions or explanation differs from what you see in the real world, you’re propelled (jetted?) back around the modeling cycle, back to the formulate stage, back around the lazy river of mathematical modeling. If this isn’t occurring, if you’re modeling activities aren’t being driven naturally around and around by this validation step, you’re not really doing mathematical modeling.
In the final part of our session, Michelle introduced a pedagogical tool that we’ve found particularly useful when engaging teachers and students in mathematical modeling. This is a tool called the “Question Formulation Technique” or “QFT” for short. It was developed by Rothstein and Santana over the course of many years and has been used in an incredibly wide variety of settings. I encourage you to visit www.rightquestion.org to learn more, or better yet, read their really excellent book on the topic:
Over the past several years, we’ve worked to find effective ways to incorporate the QFT into the teaching of mathematical modeling. The genesis of this idea was my stubborn insistence on defining mathematical modeling as “the art of asking good questions” and Michelle’s equally stubborn insistence on saying “What the hell does that mean?” As we thought about this carefully, we gradually realized that students often struggle with mathematical modeling in the same way that they struggle with mathematical proof – they’re stuck at the beginning, stuck at “Where do I start?” With modeling, clearly defining the questions your’re trying to answer, learning to identify the types of questions that modeling can answer, and identifying the questions you need to answer in order to build a model are all crucial steps. These occur right smack at the start of the process, somewhere within that “Problem” box and along the way to that “Formulate” step. What we’ve found is that using the QFT at the start of the task, or strategically at points along the modeling cycle, is a really good way to get students to think deeply about these questions, own these questions, and be motivated to answer these questions.
If you’d like to read a little bit more about our work with the QFT and mathematical modeling, here’s a draft article we’ve been working on.
My guess is that this isn’t going to make it much past the draft stage, as we’re now shifting to work on our new book on mathematical modeling. Ah, that’s a perfect segue to what was the biggest highlight of the week for us – signing a contract with Math Solutions to publish this book. It’s tentatively titled “Model with Mathematics” and we’ll keep you posted on progress here. We’re both very excited to be working with the Math Solutions team on this project and looking forward to sharing more of what we’ve learned about learning and teaching mathematical modeling with the community. So, stay tuned!
Finally, just wanted to say a special thanks to everyone who attended our session. What a great crowd! As always, please feel free to contact us with any follow-up questions or comments. We’d love to hear from you.
John