In addition to having the opportunity to work with mathematics teachers implementing mathematical modeling in their classrooms, I also often have the opportunity to work with groups of teachers from across math and science who are trying to implement “STEM” ideas in their teaching or in extra-curricular activities. This has given me the chance to think through the notion of STEM and in particular, to think carefully about the role of mathematics and mathematical modeling in the K-12 teaching of STEM.
One of the most useful articles I’ve found for understanding the “big picture” and history of “STEM” is an article called “Evolution of STEM in the United States” by Professor Emeritus William E. Dugger, Jr., of Virginia Tech. Dugger carefully defines each of the letters in the acronym “STEM.” He offers that:
S – Science, which deals with and seeks the understanding of the natural world, is the underpinning of technology.
T – Technology, on the other hand, is the modification of the natural world to meet human wants and needs.
E – Engineering is the profession in which a knowledge of the mathematical and natural sciences gained by study, experience, and practice is applied with judgement to develop ways to utilize economically the materials and forces of nature for the benefit of mankind.
M – Mathematics is the science of patterns and relationships.
Within these four definitions one already begins to see the interrelated nature of these areas and their dependence upon one another. Readers of this blog will also note his characterization of mathematics as the science of pattern and relationships; again, this way of thinking about mathematics illuminates the deep connections and utility of mathematics for S,T, and E.
Dugger also offers several models of the way STEM is, or can be taught. The first of these is the “silo model,” where we view STEM as “S-T-E-M,” with each discipline being fully distinct and independent and taught with no integration among the four. The second is similar, retaining the silo nature, but emphasizing some disciplines more than others. Dugger labels this one as “S-t-e-M,” with the upper and lower case indicating levels of emphasis. A third model occurs when one of the four disciplines is integrated into the other three. The most common is when the “E” is integrated into the rest. Dugger denotes this as “E -> S,T,M.” Here, the S,T, and, M, remain in silos, but the E is integrated into each. Dugger’s final model is the fully integrated approach, where each of the four are integrated into one another. This, in effect, has us view STEM as a “meta-discipline” and this kind of integration can be simply denoted as “STEM.”
When I work with STEM councils or groups working to create STEM opportunities for students, it’s this last model that I emphasize. For me, this “meta-discipline” or integrated approach is what’s necessary if our students are going to be able to work effectively in the scientific community of today and contribute to the solution of our most pressing challenges. Nature recently released a special issue on interdisciplinarity with the subtitle “Why scientists must work together to save the world.” This is just one more voice in the chorus of voices calling out for bridges between the myriad array of disciplines created as a result of fifty years of hyper-specialization. Helping students experience an interdisciplinary perspective and be prepared to work in interdisciplinary teams seems like a worthwhile goal for those working to create STEM opportunities for students. Note that this doesn’t diminish the importance of the disciplines or obviate the need for deep content knowledge, but rather, creates opportunities to bring that content knowledge to bear on problems that can’t be solved by working solely within disciplinary boundaries.
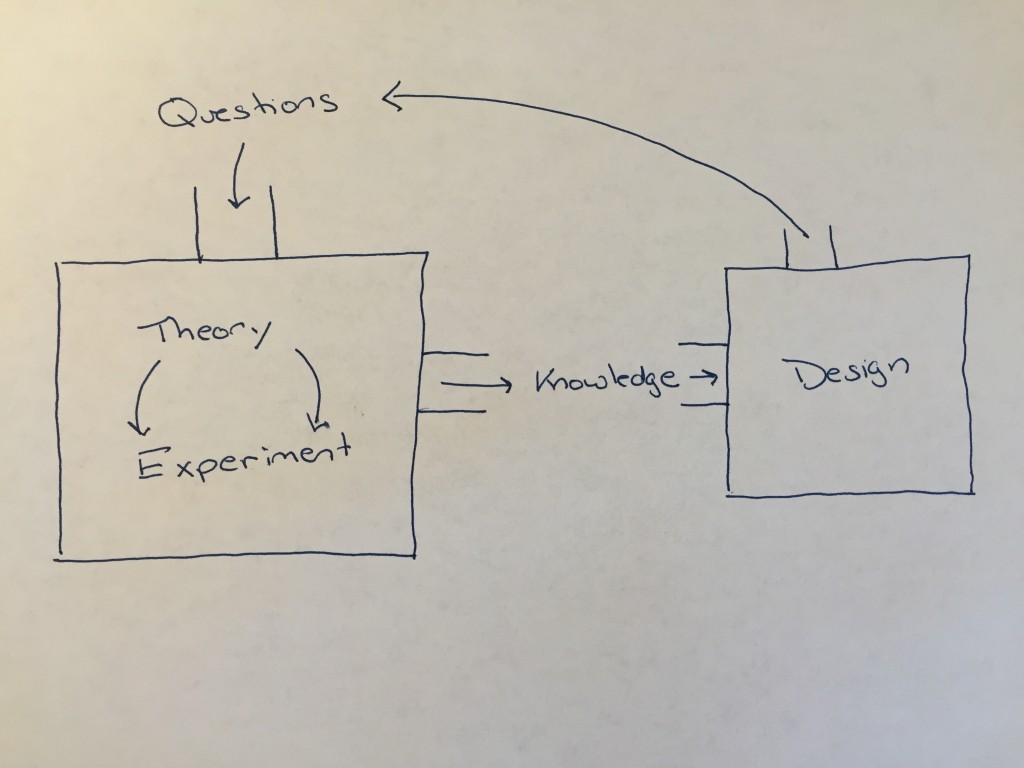
This, of course, bring up the challenge of actually doing this in practice in K-12. What does a good STEM activity actually look like? The risk is that we create activities where students do a little “S” and a little “T” and then a little “E” and then we throw in a little “M” and we’re back to the “S-T-E-M” model rather than the “STEM” model. To help people think about “STEM” vs. “S-T-E-M” and designing good STEM activities, I encourage them to think in terms of the three central practices of STEM. In shorthand, we can think of these three practices as theory, experiment, and design. You may be more comfortable thinking of these in terms of cycles that you’ll find in the NGSS and CCSSM, namely, the mathematical modeling cycle, the engineering design cycle, and the scientific method. One way to picture the relationship among these cycles or among the practices of theory, experiment, and design is:
That is, we have questions about the real-world. We use the tools of science to find explanations and build the ability to make predictions. These tools of theory and experiment, or modeling and experiment, generate knowledge about the world. We take this knowledge and use that to design technology that lets us control and modify our world. Doing so often creates new questions that we then again turn to theory and experiment to explore, and so on.
A good STEM activity engages students in this sort of interplay of the central practices. The starting point can be anywhere in the diagram but shouldn’t stay confined to a particular box. In practice, it’s often easiest and most easily engaging to start in the “design” space, that is, to start with what we might think of as an engineering challenge. But, a really good engineering challenge will have students asking questions that they need to turn to theory and experiment to answer. They’ll get a deep sense for how science informs engineering and how engineering challenges lead to interesting scientific questions. And, along the way they’ll engage in mathematical modeling, engineering design, and the practice of science.
Now, this is still all rather abstract! Next time, I’ll make this very concrete and we’ll explore a particular STEM challenge and see exactly how the interplay pictured above might look in an activity appropriate for K-12 students. Till next time!
John