Mathematics is the science of pattern and when we are doing mathematical modeling, we’re extending or tying the investigation of pattern explicitly to patterns in the real world. These might not be clear, simple, spatial patterns like those that usually occur to us when we hear the word “pattern.” They might be patterns in time, or patterns in some observed data set. But, sometimes, like in the case of the so-called “Fairy circles of Namibia,” they just might be clear, simple to observe, spatial patterns in nature.
Recently, these fairy circles were back in the news due to an article about their origin that appeared in Ecography. Science News published a short piece on fairy circles, covering a bit of the history of the search for an explanation, and an update on recent thinking. Their article, titled “What fairy circles can teach us about science,” got me to wondering what fairy circles might teach us about mathematical modeling.
So, today, I’d like to explore fairy circles, how we might approach this phenomena as a mathematical modeler, and hopefully demonstrate how a question still open to modern science can be accessible to investigation in the high school math classroom. I want to do this in some detail, so, fair warning, this will be a multi-post sort of investigation.
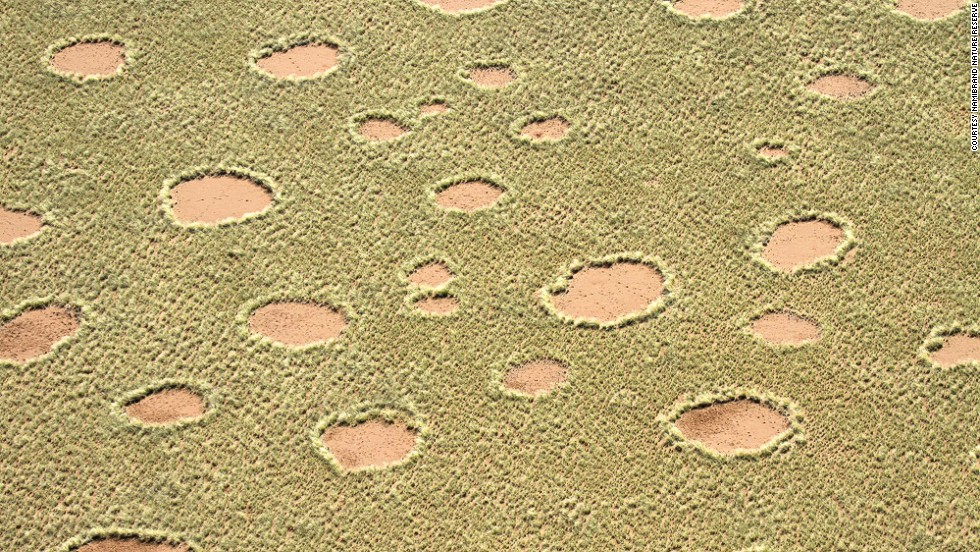
Let’s start by just looking at fairy circles. Following is a picture of the phenomena from an article by CNN addressing the topic. You can find plenty of such pictures with a simple Google of “fairy circle Namibia.”
I think the picture makes the basic phenomena quite clear. You’re looking at a section of desert, where the green is plant life, and the open circles are simply bare spots, devoid of plants. These circles dot the landscape of a 2000 km long strip of desert, each circle somewhere between 5 m and 10 m in diameter, and the circles grow, shrink, disappear, and reappear in time. The question of course is – why the heck are there bare circles?
They get their name of “fairy circles” from the explanation that they are created by gods, spirits, or fairies. The image of thousands of fairies deciding to take a break, landing in the desert, and creating a nice little circular clearing for themselves is an appealing one. Over time however, various alternative theories have been proposed. These include toxic soil, termites, and radioactivity. They also include the idea that these patches are the result of self-organization, and that they occur naturally as the result of competition for scarce water resources between plants in the desert. This is the hypothesis that I’d like to investigate here.
The idea of self-organized pattern formation is generally attributed to Alan Turing. Yes, the same guy that cracked the Enigma machine, invented the computer, and who was so ably portrayed by Benedict Cumberbatch in The Imitation Game. (If you haven’t seen it, great movie!) Among other things, Turing was interested in patterns that occurred in living systems. That is, things like the stripes on a zebra or the spots on leopard. In a paper called “The Chemical Basis of Morphogenesis,” he showed how the processes of chemical reaction and diffusion could combine, under the right circumstances, to create sharp spatial patterning. This early paper triggered years of investigations by scientists into pattern formation based on this mechanism and related mechanisms. The mathematician Jim Murray captured a huge amount of this work in his excellent book “Mathematical Biology.” Now, the first point I want to make is that Turing’s investigation, and most of the subsequent investigations into pattern formation have been carried out via mathematical modeling. This area of pattern formation in living systems, given that mathematics is the science of pattern, has been an incredibly ripe and fruitful area for the mathematical modeler.
So, back to Namibia. When a mathematical modeler sees a spatial pattern, like fairy circles, they think “self-organization.” Now, what does that mean? Well, in general, that means they are inclined to look for some underlying physical mechanism, usually some form of competition between effects or between things, and then to see if this mechanism can indeed drive the system toward forming a pattern spontaneously. From the work of Turing and all those who followed him, they know that this isn’t unlikely. In fact, they know that lots of spatial patterns in nature, from the stripes on a zebra to the patterns created by the growth of bacteria in a Petri dish can be understood in this way. So, seeing fairy circles and hearing the hypothesis of self-organization as an explanation is a perfectly reasonable thing for the modeler. Their job is to then see if they can test this hypothesis by mathematizing the proposed underlying physical mechanism, and then analyzing the mathematical model to determine if there are conditions under which spatial patterns will indeed form. In this way, they are testing the hypothesis that the proposed physical mechanism can lead to the patterns observed. If their model can be shown to not lead to pattern formation, then they’ve ruled out the proposed mechanism as the sole cause of the patterns. If it can be shown to lead to pattern formation, then the mathematical conditions under which this happens can be checked against the real world, either strengthening the case for the proposed mechanism or suggesting refinements to the model.
This is the approach taken by Getzin et. al. in the Ecography paper mentioned above. They’ve built a mathematical model that “supports the hypothesis that fairy circles are self-organized vegetation patterns that emerge from positive biomass-water feedbacks involving water transport by extended root systems and soil-water diffusion.” Okay, that’s a mouthful, and their mathematical model is pretty darn sophisticated. It’s a system of non-linear partial integro-differential equations for… well, it’s complicated. So, why would I claim this is a problem appropriate for the high school classroom?
Ah! That’s a pretty good cliff-hanger, so let’s break here for today and pick up next time with this question. In the meantime, perhaps you might think about how your students might think about this problem. That is, suppose you told them about fairy circles and that competition between plants was a proposed mechanism behind the patterns. How might they investigate this through mathematical modeling? How might you? Till next time…
John