How many piano tuners are there in the United States? How many golf balls would it take to circle the earth at the equator? How many ping-pong balls would fit in the Superdome?
We’re often asked if questions like these are the basis for a good modeling exercise or if a student answering questions like these is engaged in mathematical modeling. My general answer? “Maybe” or, “It depends.” Today, I’d like to explore this question a little bit and think through how such questions can be a way to engage students in the art of mathematical modeling and what it takes to investigate one of these questions from a modeling point of view.
Problems like these are often referred to as “Fermi Problems” after the Italian physicist and Nobel Laureate, Enrico Fermi. Fermi was known for his ability to make quick, remarkably good, estimates to answer questions like these. Sometimes we refer to the calculations involved as being “back-of-the-envelope,” indicating a sort of rough order-of-magnitude estimation procedure for obtaining estimates. Sometimes, these types of questions become interview questions at firms like Google, purportedly to test a candidate’s ability to think quickly and reason quantitatively. There is no doubt that this skill of estimation is an important part of what we mean by “quantitative reasoning,” and there is no doubt that quantitative reasoning is an important skill for mathematical modeling. But, is an investigation of a Fermi Problem the same thing as doing mathematical modeling?
To answer this question, let’s take a particular Fermi Problem and think about two different investigations, one which stays pretty clearly embedded in the realm of quantitative reasoning and a second which shows how we might develop such a problem and push our students to genuinely take a modeling perspective on the question. Since ping-pong balls are always fun and generally familiar, lets take up the question – how many ping-pong balls would fit in the Superdome?
Now, one way to think about answering this question would be to simply take the volume of the Superdome and divide by the volume of a ping-pong ball. In pre-Google Fermi days, we’d need to figure out how to estimate both of these quantities, but now we can get good estimates of these two volumes with just a few keystrokes. Since the first numbers that Google gave me were in cubic feet, I’ll work in these units. I found:
Volume of Superdome ![]()
Volume of a ping-pong ball ![]()
Dividing, I obtain:
Number of ping-pong balls in Superdome ![]()
And, I’m done. Generally, with most Fermi problems, one says “wow, that’s a lot of ping-pong balls,” and the discussion ends.
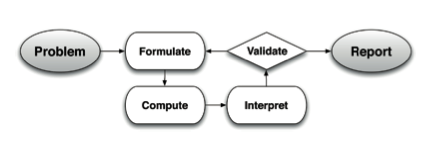
Now, let’s think about what we just did in the context of the modeling cycle.
We started with “Problem,” i.e., how many ping-pong balls would fit in the Superdome? We can argue that we moved to “Formulate” when we said “divide the two volumes,” but that already feels a little forced. We could argue that we went through the “Compute” stage and perhaps even the “Interpret” stage when we took our final number and said “almost 57 billion ping-pong balls” as an answer, but that feels even more forced. And, what about that “Validate” part? What about comparing back to the real-world? What about the whole cyclic nature of mathematical modeling? I’d argue that if this is the type of discussion around a Fermi Problem, then, no you’re not really doing mathematical modeling. That’s not to say that you’re not doing something valuable, but at the same time, you’re not really involving your students in mathematical modeling and you’re not really training them in thinking like a mathematical modeler.
So, the question becomes – what would an investigation of this problem look like if we really wanted to use it as a way of having students experience the art of mathematical modeling in a more genuine manner?
Consider an alternate approach. We begin, as before, by reasoning about volumes. This time, perhaps, we introduce a little notation, and think about the question a little more generally. For example, we might say the number of ping-pong balls, ![]() , that fits in a given space is a function of the volume of the space,
, that fits in a given space is a function of the volume of the space, ![]() , and the volume of a ball,
, and the volume of a ball, ![]() . That is,
. That is,
![]()
Now, our initial model of this dependence is as before:
![]()
Why is this different than what we did before? Well, in one way, it’s not. We could repeat the steps from before, substituting in the same estimates as above for ![]() and
and ![]() and obtain, of course, the same answer. But, expressed this way, we can also more easily think about this functional dependence that so often lies at the heart of mathematical modeling. If I increase the volume of the ball,
and obtain, of course, the same answer. But, expressed this way, we can also more easily think about this functional dependence that so often lies at the heart of mathematical modeling. If I increase the volume of the ball, ![]() decreases in an inversely proportional way. If I increase the volume of the space,
decreases in an inversely proportional way. If I increase the volume of the space, ![]() increases in a directly proportional way. This hypothesized functional relationship makes intuitive sense. Written this way, I can also easily think about model validation. While I can’t afford fifty-six billion ping-pong balls nor get away with filling the Superdome with ping-pong balls, I can fill a shoe box. I can actually do that experiment, fully, and compare it to my model’s prediction. This will give me a sense of whether or not my model is realistic and believable. And, if I do that, I’d find that my model overestimates the number of balls I could fit in a shoe box (or any box) by about 25%. This would likely lead me to realize that ping-pong balls don’t pack together without gaps, and I’d be driven around the modeling cycle, and inclined to modify my model, perhaps by including a space filling scale factor:
increases in a directly proportional way. This hypothesized functional relationship makes intuitive sense. Written this way, I can also easily think about model validation. While I can’t afford fifty-six billion ping-pong balls nor get away with filling the Superdome with ping-pong balls, I can fill a shoe box. I can actually do that experiment, fully, and compare it to my model’s prediction. This will give me a sense of whether or not my model is realistic and believable. And, if I do that, I’d find that my model overestimates the number of balls I could fit in a shoe box (or any box) by about 25%. This would likely lead me to realize that ping-pong balls don’t pack together without gaps, and I’d be driven around the modeling cycle, and inclined to modify my model, perhaps by including a space filling scale factor:
![]()
We could now think about and explore how this scale factor, ![]() , depends on the shape of the object filling this space. That is,
, depends on the shape of the object filling this space. That is, ![]() takes one value for a sphere, but a very different value for a cube. We could even now think about our modeling efforts from both a descriptive and analytic view point. From a descriptive viewpoint, we could fill different sized boxes with ping-pong balls, gather data, and fit a curve to this data. How does this curve match with our proposed analytic model above? When we think about the analytic model we’ve proposed, we could think about the underlying principles about the real-world we’ve had to posit in order for this model to make sense. For example, we’re relying on a “ping-pong ball exclusion principle” that says no two ping-pong balls can occupy the same space at the same time. We’re assuming that the Superdome is empty and ignoring all those bleachers already filling the space. We’re also assuming the ping-pong balls don’t deform under the weight of those above them. Would this really hold true in the Superdome?
takes one value for a sphere, but a very different value for a cube. We could even now think about our modeling efforts from both a descriptive and analytic view point. From a descriptive viewpoint, we could fill different sized boxes with ping-pong balls, gather data, and fit a curve to this data. How does this curve match with our proposed analytic model above? When we think about the analytic model we’ve proposed, we could think about the underlying principles about the real-world we’ve had to posit in order for this model to make sense. For example, we’re relying on a “ping-pong ball exclusion principle” that says no two ping-pong balls can occupy the same space at the same time. We’re assuming that the Superdome is empty and ignoring all those bleachers already filling the space. We’re also assuming the ping-pong balls don’t deform under the weight of those above them. Would this really hold true in the Superdome?
If we returned to the modeling cycle and tested our thinking against the cycle with this approach to the problem, I think we’d be able to convincingly argue that we’re genuinely making use of an iterative modeling approach this time around. Now, that’s kind of interesting – after all, in both cases we’re ostensibly solving the same problem. How can it be that in one case we’re “modeling” and in the other, we’re not? The key is that modeling is not just about your choice of problem. Modeling is both about the choice of problem AND the approach you take to solve that problem. Remember we build mathematical models to explain and predict. In the second approach to our ping-pong ball problem, we’re not seeking a number or an estimate as much as we’re seeking insight and understanding.
If we take the time to do Fermi Problems in the second way described above, and carefully pick the types of Fermi problems we think about, I do think that the investigation of at least some such problems can provide a valuable way to introduce students to the process of mathematical modeling. They have the advantage of being easily understood as problems and of relying on extra-mathematical knowledge that’s likely to be in the toolbox of even young students. I encourage you to attempt some Fermi Problems with your students and try them from a modeling perspective.
John
Nice, helpful distinction. I was also thinking, “that’s a lot of ping pong balls” 🙂
If we stacked them end to end, we could have them run from here to the moon about six times. Hey, a ping-pong ball ladder to the moon!
One nice feature of this particular problem is that the initial formulation is relatively straightforward (divide volume of the super dome by the volume of a ping-pong ball), and that this straightforward formulation can be seen to be inadequate relatively easily. This might be something to think about in terms of “good” modeling problems.
I also think that the nice thing about modeling the way John describes it is that failure, instead of being a problem, is an essential element of the process.