Last week, I had the opportunity to spend a few hours working with folks at Delaware’s Appoquinimink school district. The group was a “STEM Council” composed of district administrators, teachers, principles and others committed to ramping up STEM activity and STEM opportunities in the district. It’s always a lot of fun for me to get to work with such a dedicated group of people and to spend time talking about STEM, modeling, and education. A good portion of our conversation revolved around the intersection of the CCSSM and NGSS and today, I ‘d thought I’d share some of that discussion here.
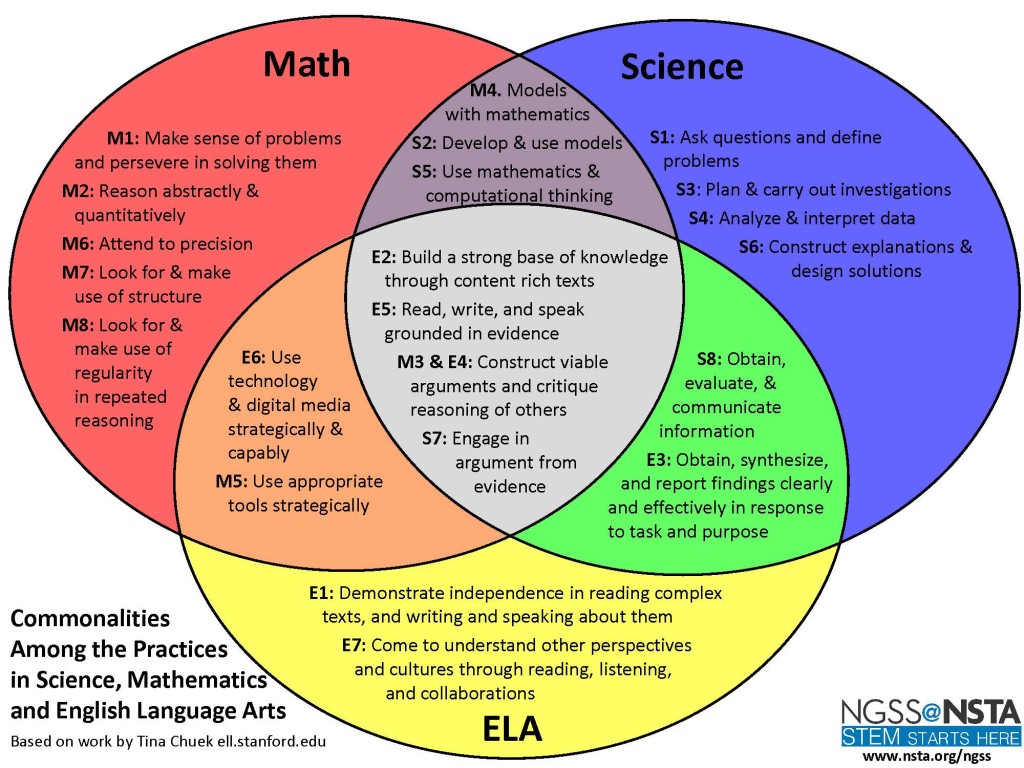
The NSTA published a Venn diagram that makes exploring the overlap in the CCSS and NGSS practices quite easy:
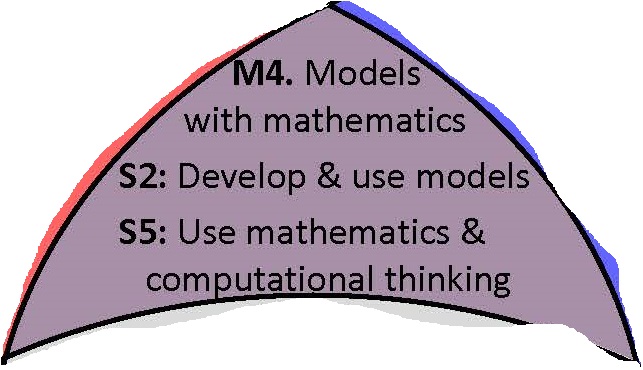
While all of the practices are, of course, crucially important, and while it is interesting to think about all the overlap regions, what’s of most interest to me is the purple region that shows the overlap between the CCSSM and NGSS:
This region is really showing us where the practices of mathematics and the practices of science overlap. It should come as no surprise that this is where the modeling standards live. Readers of this blog are certainly familiar with the CCSSM SMP #4, i.e. “Model with mathematics,” but may perhaps be less familiar with the parallel standard in the NGSS, S2, “Develop and use models.” It’s important to note that S2 is actually broader than SMP 4. When the NGSS says “Develop and use models” they are talking about both mathematical models and other types of models. While one can certainly make a strong argument that mathematical models are the most important types of models that scientists use, it is useful to explore some of these other types of models and to understand a little bit about modeling more generally than as described in the CCSSM.
Why should we bother to think about these “other” types of models? I’ll argue that besides often being useful in and of themselves, having broad knowledge of “models” and “modeling” makes one a better teacher and doer of mathematical modeling. Many of these other models and modeling approaches are more intuitive and more accessible than mathematical modeling and a discussion of these can serve as an entry point into mathematical modeling. At the same time, when we do mathematical modeling, we’re often also, consciously or unconsciously, using other types of models in our process. When I work with groups like Appoquinimink’s STEM Council, we often explore four “other” types of routinely used models so that folks can consciously add these to their toolbox and think about how they use them and how they can be used as part of a mathematical modeling process. Here’s a brief description of the four types of models we talk about:
Scale Models – This is the one with which most people are already familiar and likely the idea that leaps to mind when someone says the word “model.” By scale model, we mean a physical representation of some real world object that is proportionally scaled to some other size. This might be an architect’s scale model of a proposed building, an astronomer’s scale model of the solar system, or a biologist’s scale model of the cell. In each of these cases, the object under study has been represented on a human scale. That is, it’s been built to a size that we can readily deal with visually. It’s been built to a size that we can take in at a glance, see as a whole, and see relevant parts as needed. In building a scale model, one makes decisions similar to those made in any modeling process. We ignore some things and focus on others. We choose what to focus on and what to ignore according as what we’re interested in visualizing or understanding and our models’ utility is dictated by these choices and decisions.
Idealized Models – The notion of an idealized model is certainly one that is used routinely by mathematical modelers, but they also serve as a useful tool for thought experiments in their own right. By an idealized model, we mean one where we conceive of a system as consisting of idealized parts that don’t actually exist in the real world. We might talk about frictionless blocks sliding down frictionless inclined planes or perfectly elastic billiard balls, or perfectly rigid rods, or one-dimensional rods and so on. None of these objects actually exist. There are no perfectly elastic balls or perfectly rigid rods, but if we want to think about the motion of billiard balls or the motion of a pendulum, it is useful to conceive of such idealized objects. We might then draw conclusions just from thinking about systems of such idealized objects (the arc of a perfectly rigid pendulum will lie on a circle) or frequently, the system we conceive of as constructed of such objects becomes the one we mathematize as we build a mathematical model.
Analogical Models – We we think about analogical models, we’re, well, arguing by analogy. We say “A is like B and B behaves as such, so perhaps A behaves in an analogous manner.” If you’re an economist you probably talk about “pumping money into the system” or “turning up the interest rates.” There is no “pump” in the world’s money supply and no knob for adjusting interest rates. What you’re doing is saying the economy is like a machine and money like something that flows through that machine. Pumping and turning knobs then become ways to think about what you are doing to the rather abstract “machine” that is the economy. We’ve talked about “toy models” before and these are too often great examples of analogical models. Our Great Lakes problem had us exploring the flow of a contaminant through three small containers. There, we were arguing that the flow of a contaminant through the Great Lakes behaved analogously.
Phenomenological Models – I always like to draw particular attention to this one because, unfortunately, it is what many people think of as being “mathematical modeling.” And, it’s not identical! Phenomenological modeling is what we do when we fit a curve to data. It’s our way of describing a data set using mathematical objects. We may do this visually or we may use mathematical tools like the method of least squares to do this fitting, but at the end, what we’re doing is describing data. It’s important to realize that we’re modeling data and that this is one step removed from the real world. This is the type of modeling that the CCSSM calls “descriptive modeling,” and so it falls into the class of “mathematical models,” but it’s important to note that it’s but one subclass of mathematical models. An important one, but just a piece of the puzzle.
If you’re a math teacher and you haven’t read the NGSS, I encourage you to do so. At the very least it’s worth reading their description of “Develop and use models.” Working together with our science teacher counterparts is a tremendous way to further the teaching and learning of mathematical modeling and exploring what we have in common (which is a lot!) is a great place to start.
John