This week, I’m in Denver Colorado for the 5th annual STEM Forum and Exposition organized by NSTA. Later this week, on behalf of NCTM, I’ll be running two short “NCTM sessions” on mathematical modeling. In these sessions, we’ll explore the question “What should the “M” in STEM look like in a good STEM activity?” Later this week, I’ll post more about these sessions and the STEM forum, but today, I want to talk about my plane ride.
No matter how often I fly, I find that looking out the window of an airplane never gets old. Given a choice, I always choose a window seat, even if it means seat 35F at the very back of the plane as it did yesterday. My choice was rewarded with a cloudless sky for most of the flight and I spent my time alternating between reading and looking out of the window. Now, if you fly from Philadelphia to Denver, or fly any other route that takes you across the mid-west you’ll see large swaths of the country that look like this:
Crop circles! Well, okay, that’s probably not the kind of crop circles you thought of when you read the title to this post. But, they’re still really cool and it’s fascinating to see the patterns laid down over thousand and thousands of acres of the United States. These crop circles are, of course, the result of what’s called “center pivot irrigation.” This is where a pumping system is built at the center of a circle, a long mobile arm of sprinklers is constructed, and this arm pivots around the central pump, irrigating a large circle of crops. If you’ve ever driven through regions where center pivot irrigation is used, you’ve likely seen the sprinkler arms:
Flying over thousands and thousands of these crop circles yesterday, I realized that there are all sorts of interesting mathematical modeling and generally more STEM questions that they present. Here are just a few that occurred to me:
The pivot arm is on wheels all along its length. At various points along this radius, motors of some sort drive the motion. Since this is a radial motion, the motors furthest out must be going faster than the motors closest to the pivot point. How is this motion coordinated? How does this need to increase the motor speed with radial distance impact the largest such circle that’s practical?
Since water is being forced from a central point, the water pressure must drop as we move outward along the radial arm. This means that if all sprinklers were identical along the arm, the crops closest to the pump would get over-watered, and those furthest out under-watered. How does one design a sprinkler system for this arm so that we deliver the same amount of water across the entire circle?
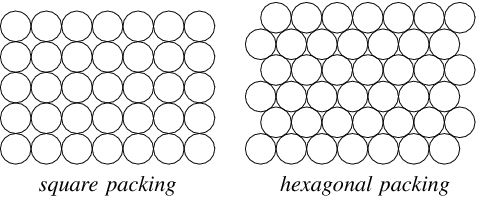
While the arrangement of these crop circles clearly must follow, to a certain degree, local topography, why are they generally arranged in a less-than-optimal packing arrangement? That is, we know that hexagonal packing of circles covers more area than the rectangular packing we observe. So, why do these circles generally follow the arrangement on the left rather than the right in the picture below?
Why are the circles that we see generally all the same size? For the most part there are only two sizes of circles one will see. Why does there appear to be a minimum circle size? We know that if we used circles of various sizes, we could cover more area as in this picture:
Why don’t farmers use circles across a greater range of sizes?
Now, as with any good mathematical modeling problem or any good STEM problem, I imagine that the answers to these questions are complex, and involve multiple factors and multiple constraints. As my flight neared Denver yesterday though, I decided to see if I could at least convince myself that there was a good reason why we don’t see small crop circles by sketching out a really simple mathematical model. This was a “back of the airplane menu” type model, but nonetheless, fun to play with and I thought I’d share it with you here today.
I wanted to see if there was an economic reason why we don’t see circles below a minimum size. That is, are circles below a certain size just not profitable? I assumed that there were three basic costs associated with constructing and running a single center pivot irrigation system:
![]()
![]()
![]()
I also assumed that the revenue one would generate was proportional to the area of the circle:
![]()
Putting this all together meant that the profit, ![]() , could be written as:
, could be written as:
![]()
Using my assumptions of proportionality to the radius, ![]() , I could rewrite this as:
, I could rewrite this as:
![]()
Here, the ![]() are positive constants of proportionality. A little rearrangement yields:
are positive constants of proportionality. A little rearrangement yields:
![]()
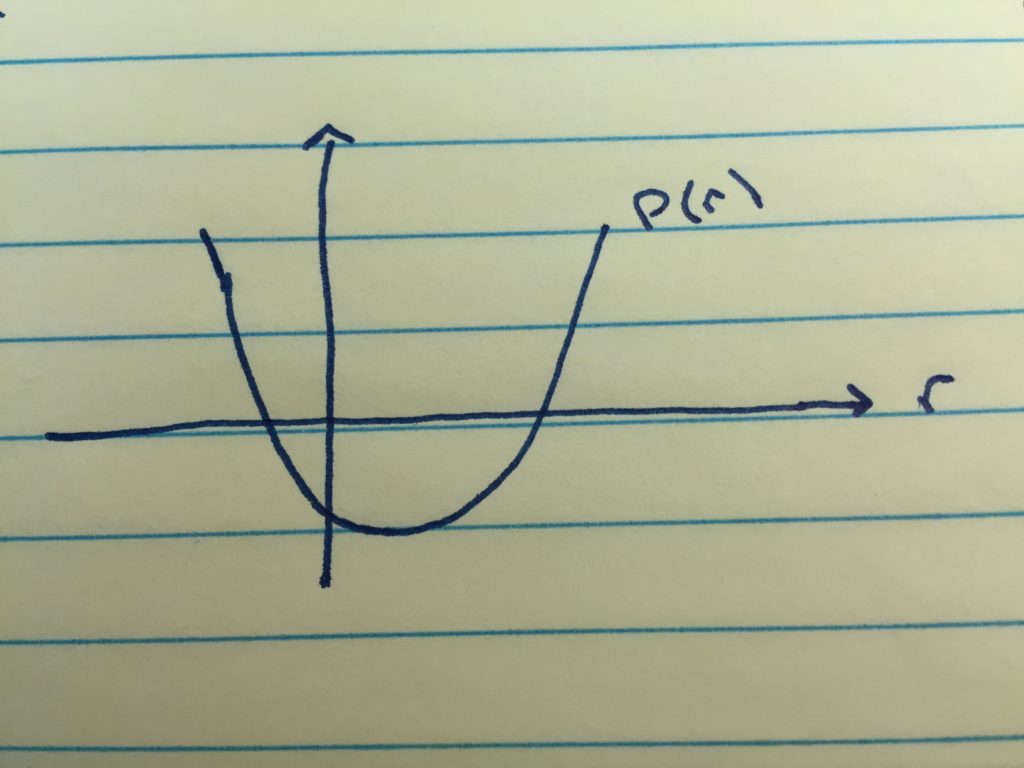
Now, ![]() must be positive, otherwise, the profit would always be negative and there would be no sense in ever having any sort of circle. Knowing that means the general shape of the profit curve as a function of r must look like:
must be positive, otherwise, the profit would always be negative and there would be no sense in ever having any sort of circle. Knowing that means the general shape of the profit curve as a function of r must look like:
The fact that this curve becomes positive only at some finite positive value of ![]() means that, yes, there is a minimum size below which a crop circle just isn’t profitable. I’m convinced that our farm industry knows what it’s doing when it avoids making teeny-tiny circles. In fact, it seems that we should be driven to make our circles as large as possible (note that real circles cover hundreds of acres) and that there must be another explanation for why we only make them up to a certain size. I suspect that the maximum size of theses circles is dictated either by the demands of designing for the pressure drop across the sprinkler array or the demands of increasing speed of the motors as we move further out along the arm. Or, probably both.
means that, yes, there is a minimum size below which a crop circle just isn’t profitable. I’m convinced that our farm industry knows what it’s doing when it avoids making teeny-tiny circles. In fact, it seems that we should be driven to make our circles as large as possible (note that real circles cover hundreds of acres) and that there must be another explanation for why we only make them up to a certain size. I suspect that the maximum size of theses circles is dictated either by the demands of designing for the pressure drop across the sprinkler array or the demands of increasing speed of the motors as we move further out along the arm. Or, probably both.
But, it was time to ask my neighbors to get up one last time so I could use the bathroom and then, quickly, my plane ride to Denver was over. I hope you’ve enjoyed my random flight musings and hope perhaps you’ve found some inspiration for some cool STEM problems here in this post. I’ll be sure to post again at least once more this week and share what I learn at this year’s STEM Forum. Till later.
John