Whenever I’m asked “What’s the most important skill for a mathematical modeler to have?” or “What do you look for in a graduate student?” or “What do you wish every entering university student would have?” my answer is always the same and always one word – curiosity. Now, that could either indicate a stunning lack of imagination on my part or it could indicate that I think this idea of curiosity is pretty important. Today, I’ll try and convince you that it’s the latter of these two, give you an example of what I mean, and along the way, develop some ideas of how to take advantage of some common technology in your classroom.

First, lets talk about this notion of curiosity. In his wonderful book “Curious: The Desire to Know and Why Your Future Depends on It,” Ian Leslie describes two categories of curiosity, distractive curiosity and epistemic curiosity. Distractive curiosity is what keeps us checking email on our phones or refreshing our Twitter feed. It’s the built in craving we all feel for the novel or the new. Easily satisfied, short-lived, and ultimately not very nourishing. Epistemic curiosity is the directed and focused, it’s the form of curiosity that grabs hold of us and and drives us to explore something deeply, with no end in mind, just the desire to really know. When I answer “curiosity” to the inquisitive parent or prospective graduate student, I’m talking about epistemic curiosity, or the unbounded longing to know. I hope you are at least a little convinced that I’m not being lazy in my answers, but rather, can see how a prospective university student, or a graduate student, or any prospective mathematical modeler at any level, would be well-served by having a high level of epistemic curiosity. Maybe next time instead of a one-word answer, I’ll hand the questioner a copy of Leslie’s book.

So, what does this have to do with golf, math, or your classroom? Let me take you along with me on a little investigation into the latest bane of my existence and we’ll explore golf, math, and some ideas for your classroom along the way. As we do so, keep in mind, it’s all driven by curiosity.

As is the case for many occasional golfers, I suffer from the dreaded slice (yes, that’s the latest bane of my existence). The beautiful, satisfying thwack of the ball is spoiled again and again as I watch my initially straightly flying shot arc to the right and end up in the trees or on a good day, the neighboring fairway. Now, a slice is caused by one of two things (or perhaps both), an outside-in swing path or an “open” club-face on contact. I’m fortunate to have golfing buddies who in-between falling over laughing manage to occasionally watch my swing for me and so I’m fairly certain my particular issue is mostly an “open” club face. Striking the ball with an open club face puts a tremendous spin on the ball and quickly the Magnus Effect takes over, causing the curved flight path. In the video below you’ll see a few creative and curious fellows illustrate the Magnus Effect with a basketball and a really high dam.

The Magnus Effect is ultimately an instance of Bernoulli’s Law which you can explore at:

scienceworld.wolfram.com/physics/BernoullisLaw

For now, let’s just agree that it would be good if I could put less spin on my golf ball. (But, note how many interesting pathways the curious could follow here!) So, to confirm this “open-club face” hypothesis and to get a handle on just how open it is, I thought it might be useful to be able to video my golf club impacting my ball during my swing. And, this brings me to a neat tool for your classroom – the iPhone 6. Remarkably, the camera on the iPhone 6 is not only of incredible quality, but can do limited high-speed photography as well. To get a grasp on just how cool that is, let me just say that about ten years ago, it cost us more than 10,000 to buy a low-end basic high speed camera for our lab. Yes, that camera could ultimately record much faster, but at an incredibly limited resolution and it’s lower end recording speeds (which were the most useful speeds!) were identical to what the iPhone 6 can now do.

The slow motion setting on the iPhone 6 gives us a frame rate of 240 fps. That is, it will capture 240 frames of video per second. The question then becomes – Is this fast enough to capture my club hitting a ball? Which, of course, brings up the question – How fast is my club head moving when I hit a golf ball? It was at this point in my thinking that I realized I had no idea how fast my club (or any club) was moving. And, this brought to mind the difference between distractive and epistemic curiosity. I could easily Google “How fast does a golf club impact a ball?” I’d get answers that would at least give me a ball park to work in. But, this is where the epistemically curious or the mathematical modeler parts ways with the non-modeler. The mathematical modeler isn’t just seeking an answer, they’re seeking insight. It’s not just a number they want (although that’s part of it), but they want a deeper understanding of whatever it is they are exploring. It’s more work then Googling, but it’s ultimately more valuable as well.

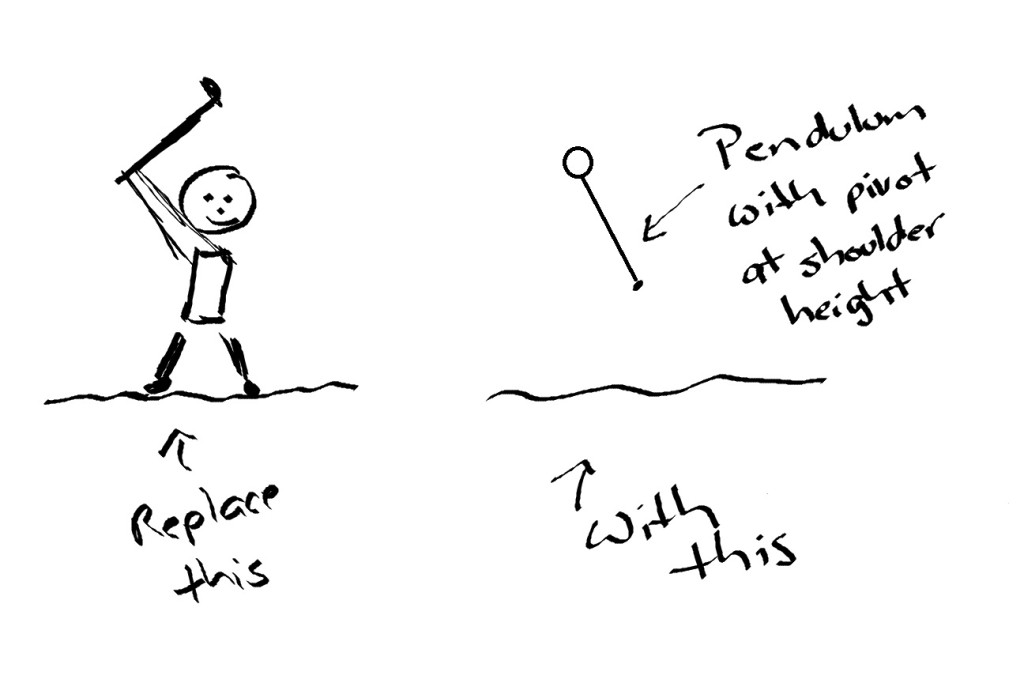
So, let’s do a little quick and dirty mathematical modeling, a “back-of-the-envelope” type analysis. We can get a lower bound on the speed of the club head at impact by idealizing the heck out of the situation. If the lower bound tells us our iPhone 6 can’t capture the impact, then we can move on. If it suggests that it could, we’ll need to improve our model to get a tight lower bound and compare again. We’ll idealize our golfer as a simple pendulum.

Now, suppose we make the assumption that all a golfer does is act like a pendulum, bringing the club head to the top of the travel path and then releases, letting gravity do the rest. Note, we know this is wrong! We know that we are ignoring everything the golfer does to accelerate the club head. That’s why this is a crude lower bound. With these assumptions, we can however quickly and easily compute a lower bound on club speed by using conservation of energy. All of the potential energy at the top of the swing is converted into kinetic energy at the bottom. That is,

(1)  

The mass terms cancel, we know the gravitational constant, and if we estimate the initial height of the club head at about 2.5 meters, we get a lower bound for the velocity of our club head of about seven meters per second (15 miles per hour). Those of you who have ever swung a golf club will see instantly that this is very much a crude lower bound. The golfer accelerates the club head through the swing and so we’d expect actual club head speed to be eight or nine times this number. But, we know it should be no slower than this and that’s enough for our calculations today.

So, can our iPhone capture our club head at the moment of contact? To resolve the motion, we can estimate that we’ll need to capture the club head as it moves centimeter by centimeter. If is our frame rate and the velocity of the object we want to capture, then the distance the object travels between frames is simply . Our lower bound on velocity and the known frame rate of 240 fps tells us that our club head is traveling at least 3 centimeters between frames. Knowing that this is a pretty crude lower bound and that the actual club head will be traveling much faster, we can confidently say that it is unlikely that even the really cool iPhone 6 camera will capture this motion. Since it’s always fun (and important) to double-check with reality, here’s a “slo-mo” video of my club hitting a ball.

Sadly, as we predicted, too fast to tell the position of my club face!

But, we’ve discovered a pretty neat new tool that I hope you’ll try out in your classroom. How can you get students playing with “slo-mo,” observing things they haven’t seen before, figuring out how fast things move in the real world, and exploring some cool mathematics along the way? Let us know! Oh, and please don’t take my comments above as being anti-Googling! It’s well worth spending some time poking around on the web searching “math model golf.” You’ll find a lot of neat work that I’m sure will give you other ideas for your classroom. Doug Arnold’s beautiful little paper on “The Science of a Drive” is a great place to start.

– John

Thought I’d share a brief article I wrote for PMENA (Psychology of Mathematics Education, North America, 2014 meeting). This is a pretty good introduction to my perspective on mathematical modeling. – John

Mathematical Modeling – A Practitioner’s Perspective

John A. Pelesko, University of Delaware

Introduction

Having spent the better part of the last twenty-five years engaged in teaching and doing mathematical modeling as an applied mathematician (Pelesko & Bernstein, 2003; Pelesko et.al., 2013), it is hard to overstate the joy I felt upon realizing the special emphasis that the new standards adopted widely across the United States, the Common Core State Standards in Mathematics (National Governors Associate Center for Best Practices & Council of Chief State School Officer, 2010), placed upon modeling. This ascension can be credited in part to the long term efforts of researchers such as Pollak (Pollak 2003, 2012), Lesh (Lesh, 2013), and others who have argued that it is not just applications of mathematics that should be incorporated into the mathematics curriculum at all levels of education, but that the practice of mathematical modeling itself is an essential skill that all students should learn in order to be able to think mathematically in their daily lives, as citizens, and in the workplace (see, e.g., Pollak, 2003). Now that the importance of mathematical modeling is being recognized by the mathematical education community at large, appearing as both a conceptual category and a Standard for Mathematical Practice in the Common Core State Standards in Mathematics (CCSSM), it is necessary that those who do mathematical modeling engage deeply with the K-12 mathematics education community around the issues of teaching and learning the practice. It is important to note that mathematical modeling is practiced far and wide – across the natural sciences, engineering, business, economics, the social sciences, and in almost every area of study in one form or another. Hence, the set of stakeholders in this conversation is large, and we should be careful not to substitute any one practitioner’s perspective for the whole. Nevertheless, in an attempt to contribute to this conversation, here I provide one practitioner’s perspective.

What is Mathematical Modeling?

Given the lack of attention that has been paid to mathematical modeling in the US educational system, especially in mathematics teacher education programs (Newton et.al., 2014), it is not hard to imagine that many mathematics educators upon reading the CCSSM found themselves asking this question. The brief description of mathematical modeling found in the CCSSM (pages 72-73) and the fact that this description first appears within the high school standards likely adds to this confusion. Further confusion is likely to occur as educators digest the Next Generation Science Standards (NGSS Lead States, 2013), which make use of the term “model” both in and out of the context of “mathematical model.”

To address the question “What is mathematical modeling?” it is then perhaps useful to first consider the question “What is modeling?” My answer? Modeling is the art or the process of constructing models of a system that exists as part of reality. By “model,” I mean a representation of the thing that is not the thing in and of itself. The model captures, simulates, or represents selected features or behaviors of the thing without being the thing. By “mathematical model” I mean a model or a representation that is constructed purely from mathematical objects. So, mathematical modeling is the art or process of constructing a mathematical model. That is, mathematical modeling is the art or process of constructing a mathematical representation of reality that captures, simulates, or represents selected features or behaviors of that aspect of reality being modeled.

Now, we should note that mathematical models have a special place in the hierarchy of models in that they have both predictive and epistemological value. The epistemological value is a consequence of the idea that mathematical modeling is a way of knowing. The predictive value of a mathematical model gives mathematical models a special place in “science,” loosely and broadly defined, in that a mathematical model can take the place of direct ways of knowing, in other words, experiment. A good mathematical model is both an instrument, like a microscope or a telescope, allowing us to see things previously hidden, and a predictive tool allowing us to understand what we will see next.

Note that an especially “good” mathematical model, that is, one with a high level of predictive success, often ceases to be thought of as “just a model.” Rather, it attains a different status in the scientific community. We don’t say “Newton’s mathematical model of mechanics,” rather we say “Newton’s Laws.” We don’t say “Schrodinger’s model of the subatomic world,” rather we say “Quantum Mechanics” or the “Schrodinger Equation.” Yet, each of these examples is, in fact, a mathematical model of the thing, and not the thing in and of itself. These examples have attained the highest possible level of epistemological value. They have become the way of knowing, understanding, describing, and talking about their subjects.

Now, we have diverged into abstract territory and we do not want to leave the reader with the impression that mathematical modeling is hard, something to be left to the Newtons and Schrodingers of the world. Rather, we hope the reader is left with the impression that mathematical modeling is exceedingly useful and that by helping our students master this practice, we will be adding a tool to their mental toolkit that will serve them well, no matter what their future plans.

Thought Tools for Modeling

The question then becomes: How exactly does someone become a proficient mathematical modeler? In the United States, as evidenced by textbook after textbook on mathematical modeling (Pelesko & Bernstein, 2003)[1], the answer has been “Modeling can’t be taught, it can only be caught.” Here, I take a different perspective and argue that it is useful to think of the mathematical modeler as having discrete “thought tools,” each of which can be discovered and taught. As a consequence, we see that many “modeling cycles” unintentionally hide much of the real work of mathematical modeling.

We borrow the term “thought tools” and this framework for meta-thinking from the philosopher and cognitive scientist, Daniel Dennett. In (Dennett, 2013) he quotes his students as having made the observation that “Just as you cannot do much carpentry with your bare hands, there is not much thinking you can do with your bare brain.” Dennett then proceeds by analogy with saws, hammers, and screwdrivers, to introduce thought tools of informal logic such as reductio ad absurdum, Occam’s razor, and Sturgeon’s Law[2]. Applying this notion of thought tools to the mathematical modeler, we argue that they must possess a set of thought tools that lie in three different categories: Mathematical Thought Tools, Observational Thought Tools, and Translational Thought Tools.

Mathematical Thought Tools are those tools we attempt to add to our student’s toolkits when we teach mathematics. These include notions such as algebraic thinking, the principle of induction, the pigeonhole principle, and any tool that lets students think about and do mathematics. Note that these thought tools are directed at mathematics and their utility is generally tied to thinking in the mathematical domain.

Observational Thought Tools are those tools we typically think of as being used by “scientists.” These include the ability to think in terms of cause and effect, to observe spatial and temporal patterns in the real world, and to look deeply at reality. Note that these thought tools are directed at the real world and their utility is generally tied to thinking in the domain of the real world[3].

Translational Thought Tools are those tools that allow the mathematical modeler to take questions formed in the observational domain and translate them into the mathematical domain and translate answers and new questions uncovered in the mathematical domain back again to the observational domain. These include knowledge of conservation laws, physical laws, and the assumptions that must be made about reality in order to formulate a mathematical model. Note that these thought tools are directed both toward reality and toward mathematics. Their utility lies in their usefulness in translating between these two domains.

In a typical “modeling cycle,” such as appears in the CCSSM, one moves from the “real world” or the “problem” to the “formulation” via a single small arrow. Buried in this small arrow is the use of Observational and Translational Thought Tools. The remainder of the cycle, up to the point of comparing results with reality, generally relies purely upon Mathematical Thought Tools. While we can argue over whether or not we are properly equipping our students with the Mathematical Thought Tools they will need in their journeys around the modeling cycle, I would argue that generally we pay little attention to the Observational and Translational Thought Tools they will need to begin their journey. Identifying, unpacking, and learning how to equip our students with these sets of tools is an essential step in learning how to teach mathematical modeling.

As an example of how the mathematical modeler wields these tools, I ask the reader to imagine drops of morning dew on a spider web. The scientist, using their observational tools, notices these droplets and wonders why they are all roughly the same size. The mathematical modeler recalls that nature acts economically and often in a way that minimizes some quantity. They cast forth a hypothesis that here, nature is acting to minimize surface area, and that leads the dew to break into droplets of nearly uniform size. They recast this observation and hypothesis into mathematical terms, already anticipating the mathematics from the presence of the notion of “minimizes” and wield their Mathematical Thought Tools to predict the size of the droplets given the presence of the dew. Comparing their predicted size with the size of actual droplets, they refine and perfect their model, and have acquired an understanding of any droplets on any spider web at any point in time.

Conclusion

Mathematical modeling is a practice worth sharing and teaching. Mathematical modeling is a powerful way of knowing the world, and it can be taught rather than simply caught. In the United States, we have much work to do in order to bring this new toolkit to our students. It will take the efforts not only of mathematics educators and applied mathematicians, but of mathematical modelers of every stripe in order to do so. Here, I have sketched out one avenue of approach that in many ways parallels recent work in unpacking the thought processes behind mathematical proof (Cirillo, 2014). A similar effort to identify and unpack the thought tools of the mathematical modeler holds the promise of helping us train a wide range of students in the art of mathematical modeling.

References

Pelesko, J. A., & Bernstein, D. H. (2003). Modeling MEMS and NEMS. Boca Raton, FL: Chapman & Hall/CRC.

Pelesko, J.A., Cai, J., & Rossi, L.F. (2013). Modeling modeling: Developing habits of mathematical minds. In A. Damlanian, J.F. Rodrigues & R. Straber (Eds.), Educational Interfaces between Mathematics and Industry (pp. 237-246). New York: Springer.

Pollak, H. O. (2003). A history of the teaching of modeling. In G. M. A. Stanic & J. Kilpatrick (Eds.), A history of school mathematics (pp. 647-669). Reston, VA: NCTM.

Pollak, H. O. (2012). Introduction: What is mathematical modeling? In H. Gould, D. R. Murray & A. Sanfratello (Eds.), Mathematical modeling handbook (pp. viii-xi). Bedford, MA: The Consortium for Mathematics and Its Applications.

Lesh, R., & Fennewald, T. (2013). Introduction to Part I Modeling: What is it? Why do it? In R. Lesh, P.L. Galbraith, C.R. Haines & A. Hurford (Eds.), Modeling students’ mathematical modeling competencies (pp. 5-10). NY: Springer.

Newton, J., Maeda, Y., Senk, S. L., Alexander, V.  (2014). How well are secondary mathematics teacher education programs aligned with the recommendations made in MET II? Notices of the American Mathematical Society, 61(3), 292-5.

National Governors Association Center for Best Practices & Council of Chief State School Officers. (2010). Common Core State Standards for Mathematics. Retrieved from http://www.corestandards.org/math.

NGSS Lead States (2013). Next generation science standards. Achieve, Inc. (on behalf of the twenty-six states and partners that collaborated on the NGSS).

Dennett, D.C. (2013). Intuition Pumps and Other Tools for Thinking. New York: W.W. Norton & Company.

Borromeo Ferri, R. (2007). Personal experiences and extra-mathematical knowledge as an influence factor on modelling routes of pupils. Paper presented at the Fifth Congress of the European Society for Research in Mathematics Education (CERME 5) Cyprus, Greece.

Cirillo, M. (2014). Supporting the introduction to formal proof. In P. Liljedahl (Ed.), Proceedings of the Psychology of Mathematics Education International Conference. Vancouver, Canada.

[1] I am as guilty of this approach as the majority of authors of textbooks on mathematical modeling.

[2] Reductio ad absurdum is the form of argument which shows that a statement is true by reducing its’ opposite to an absurd conclusion and is closely related to proof by contradiction. Occam’s Razor is the principle that the simplest explanation is the most likely. Sturgeon’s Law is stated succinctly as “Ninety percent of everything is crap.”

[3] Note again that Observational Thought Tools require real-world experience. This is closely linked to the idea of “Extra-Mathematical Knowledge” being necessary for doing mathematical modeling. (See Borromeo Ferri, 2007)