By now, you’re likely familiar with the modeling cycle introduced in the Common Core State Standards.
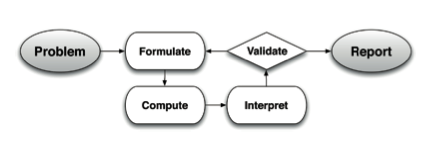
Today, I want to explore this notion of “modeling cycle” a little bit and urge you to think a little bit differently about this idea. One trend I’ve noticed in the mathematics education community is the deconstruction of this cycle or the listing of the parts like this:
(1) Problem
(2) Formulate
(3) Compute
(4) Interpret
(5) Validate
(6) Report
The point is usually made that these are all related to key skills that the mathematical modeler must possess and I wholeheartedly agree with that idea. It’s when the point becomes “these are all key steps in the modeling process” that I start to grow concerned.
Something I’d urge you to keep in mind as you study the teaching and learning of mathematical modeling is that the modeling cycle is not the same thing as mathematical modeling. Now, that sounds a little funny, so let me say it another way. The modeling cycle is simply a model of the process of mathematical modeling and as with all models, we have to be sure not to confuse the model with thing in and of itself! As with all models, the modeling cycle is incomplete, provisional, rests on assumptions that are open to question, and should be used carefully, with all of these points in mind.
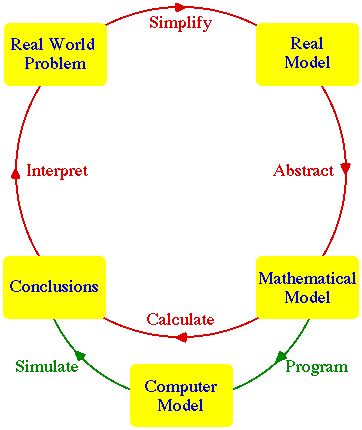
If you’ve ever Googled “mathematical modeling cycle” you’ve likely gotten an inkling of this point and encountered other modeling cycles like this one from the Stepping Stones project at Indiana University:
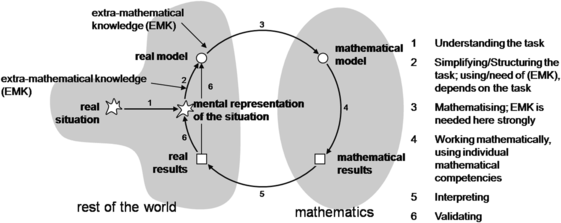
 Or this one from Rita Borromeo Ferri:
Or this one from Rita Borromeo Ferri:
Hopefully, seeing these different modeling cycles drives home the point that there is no single “modeling cycle” that is any sense “the” modeling cycle, but rather, they are all just different ways to model the process of mathematical modeling.
Recognizing this distinction, or failing to recognize this distinction, has implications for how we teach the art of mathematical modeling. Don’t fall into the trap of believing that the modeling process can be deconstructed into a list of “steps” to follow! Just as when scientists are doing science, they aren’t holding some poster version of the scientific method in their head and going through a linear process, the mathematical modeler isn’t going through a simple checklist either. More likely, they are moving fluidly between steps in a variety of orders, skipping steps, creating new steps, and doing a whole bunch of things that are represented merely as lines connecting steps in a typical modeling cycle.
The primary implication then for teaching and learning is this – don’t attempt to teach the art of mathematical modeling by having your students mechanically plod through the steps in some modeling cycle! Rather, engage them in mathematical modeling through the joint investigation of genuine modeling situations and later use the modeling cycle as a tool to engage them in meta-thinking about what they did and didn’t do during their investigation. Feel free to use whichever modeling cycle best fits your classroom! And, always keep in mind, that the modeling cycle is after all, just a model.
I think a problem we create in education is that we often skip too quickly to mathematical modeling without establishing a compelling connection to real world problems. This results in students performing half-heartedly with the lingering question, “How am I ever going to apply this in my life?”
Yes, problems are often too complicated so we need to create incomplete, provisional models to take them on. In early genetic research, for example, reproducing worms, fruit-flies, and beans provided simplified means to address complex questions about genetics.
We eventually work with more manageable, simplified “toy” or analogous models but we need to feel that it will actually help us understand something important in the real world. Pizzas, balls and ramps are “real” things but the premises being explored must also be “real” to make it a “real world” problem.
I’d like to explore what kind of guidance we can give teachers to present real world problems that don’t feel contrived and superficial and will actually be taken seriously by students.
Excellent point! One thing I did not emphasize at our PD last week very well was what the analytic model of the Great Lakes problem told us. That is, even doing the toy problem revealed the importance of the ratio R/V where R is the flow rate and V the volume of the lake. That one ratio dictates entirely the renewal rate of any size body of water that roughly acts under our toy model assumptions. I should have emphasized that more clearly! It would be good if one does this in class, to do as you suggest and have students take the insights they gain with the simplified world and see how far they can push them in understanding the full, real-world situation!