Often in mathematics, and certainly often in mathematics class, we think in terms of direct problems.  That is, we’re given something to “solve,” we’re required to find a path to a “solution,” and that’s where we end up. For example, we might be asked to find the solutions of the following equation

and we proceed by using the quadratic equation or completing the square or some such method, and arrive at values for . If we think of this in terms of applications, we often pose direct problems as well. Here, for example, we might say, suppose we drop a ball from a height , we assume air resistance is negligible, how fast is the ball traveling when the ball hits the ground? Or perhaps, how long will it take the ball to hit the ground?

But, often, in the real world, our problems aren’t formulated like this. Rather, we’re faced with problems that are posed the other way around. That is we’re faced with what are called inverse problems.  In these problems, what we’re given is the solution and what we have to do is figure out where it came from. You’re likely familiar with such problems, but perhaps haven’t thought of them in this way before. One common example is the “sonar problem” or the problem of echolocation. If I’m a bat, what I do is make a noise, and then listen for the reflected sounds that come back to me. What I then try and do is figure out the direction, location, and perhaps shape, of the objects in the environment that caused the particular patterns of reflected sounds that I heard. That is, I’m given the solution, i.e. the reflected sounds I measured, and have to figure out the problem, i.e. what pattern and shape of objects in the environment would cause that set of reflected sounds?

Such problems are an important class of problems that the mathematical modeler must be equipped to deal with. And, such problems, can be a source of challenging and engaging problems for students learning the art of mathematical modeling. Today, I’d like to explore a few simple versions of such problems and how you might use them in your classroom.

One of my favorites is a problem that was posed by Isaac Newton in Universal Arithmetik and was discussed by Groetsch in his text Inverse Problems: Activities for Undergraduates. Newton posed the problem like this:

A Stone falling down into a Well, from the Sound of the Stone striking the bottom, to Determine the Depth of the Well.

The unusual capitalization is Newton’s and apparently the style of the time was to state commands rather than pose questions. Today, we might state the problem as:

Can we determine the depth of a well by dropping a stone into the well and listening for the sound of the stone striking the bottom?

Why is this an inverse problem? Well, what we’re asked to do here is to take information we obtain at the end of a process, i.e. the time interval between us releasing the stone and it us hearing the stone strike the bottom of the well, and to infer how the stone must have traveled and from this deduce the depth of the well.

This particular inverse problem can be approached by solving the direct problem, which requires us to build a mathematical model of the time which elapses between the release of the stone and us hearing the sound of the stone striking the bottom of the well. We can imagine that we release the stone and start a stopwatch at the same instant. When we hear the sound, we stop our stopwatch and call that elapsed time, . Further, we can suppose that can be divided into two parts, the time it takes the stone to fall, , and the time it takes the sound to travel back up the well, . Our measured time is then the sum of these two:

Our job is then to build a model of the fall and the travel of the sound that lets us express and in terms of the depth of the well, . It’s worth noting that both modeling the fall and understanding the fact that sound travels at a finite speed fall within the scope of the NGSS standards and so, should be within reach of the high school classroom. I’ll skip the details here, but you should be able to arrive at an expression that looks like:

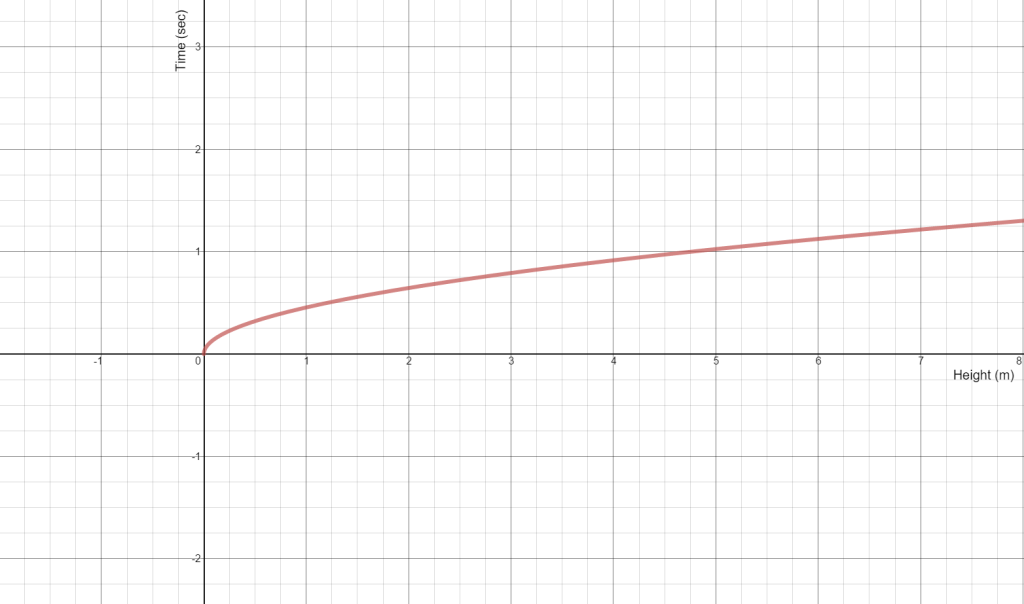
Here, is the gravitational acceleration and is the speed of sound in air. A quick plot of as a function of yields: (plot prepared with Desmos)

Now, given a measured time, , all one needs to do is draw a horizontal line on this plot at that value of time, find the intersection point with the curve shown, and read off the value of , the predicted depth of the well. It’s  worth a conversation as to whether or not the term is important here or when it may be important. It’s also worth taking time exploring how an error in the measurement of translates into an error in the prediction of . The sensitivity to such error that one sees in this problem is a typical feature of inverse problems.

If you do decide to introduce your students to the notion of inverse problems, it is worth spending at least a few minutes sharing with them the many areas of application where such problems arise. I’d suggest focusing on medical imaging as this is likely familiar territory in some sense, but unfamiliar territory in the sense of them understanding that most of modern medical imaging rests on building mathematical models and solving inverse problems.

I’ll leave you with one last inverse problem that is readily understood, but challenging to investigate. Imagine I tell you that I have a container of some sort but that I’m going to keep that container hidden in a box and not let you see it directly. However, what I will do is pour any volume of water you’d like into the container and tell you the height to which the water fills this hidden container for that volume. I’ll do this as many times as you’d like and give you as much data of this form as you want. The question is then this – can you tell me the shape of my container? Suppose I told you the container had rotational symmetry. Would that help?

I hope that this small taste of inverse problems has inspired you to consider this very important class of problems as you work to build mathematical modeling into your classroom practice. As always, we’d love to hear about your successes and challenges with this or other mathematical modeling investigations.

John